Ranzha's Skewb Method — For Beginners

Hello! If you're a beginner to Skewb solving, here's the place to be! I recommend that you know how the Skewb turns as well as notation. You don't need to know how to solve a Skewb before looking at this tutorial, but I'd recommend having a working understanding of how the puzzle operates before looking into this method. The goal of this tutorial is to by the end have a solved Skewb.

Jump to: Step One | Step Two | Step Three | Step Four


Step One: The Petrus Block

The Petrus Block consists of two square-shaped center pieces positioned adjacent to each other, along with their two corresponding corner pieces in between.
This step can be solved optimally in no more than five moves and is completely intuitive. However, as this is a tutorial for beginners, a beginner's intuition may not serve to keenly as to the formation of the Petrus Block.
For this reason, below are some substeps (with inspiration from Mike Tryczak) that should aid in Petrus Block building.

1 center + 1 Corner

The first thing to look for when solving the Petrus Block is to see if any center pieces are paired up with a corresponding corner piece. The vast majority of the time, this will already be done for you. If not, it will take only one move to connect.

Forming the Rest of the Block

As pictured above, the rest of the Petrus Block can be built in either of two directions. For the sake of the tutorial, we'll stick to building towards the left. The reasoning behind this is that after this step, and for the rest of the solve, we will hold the Petrus Block in the top-left of the puzzle.

Since we're going to be attaching two pieces to our current block from substep 1a, it should be noted that there are three ways of doing this, two of which are beginner-friendly. Here they are:

Attach the center first, and then the corner.

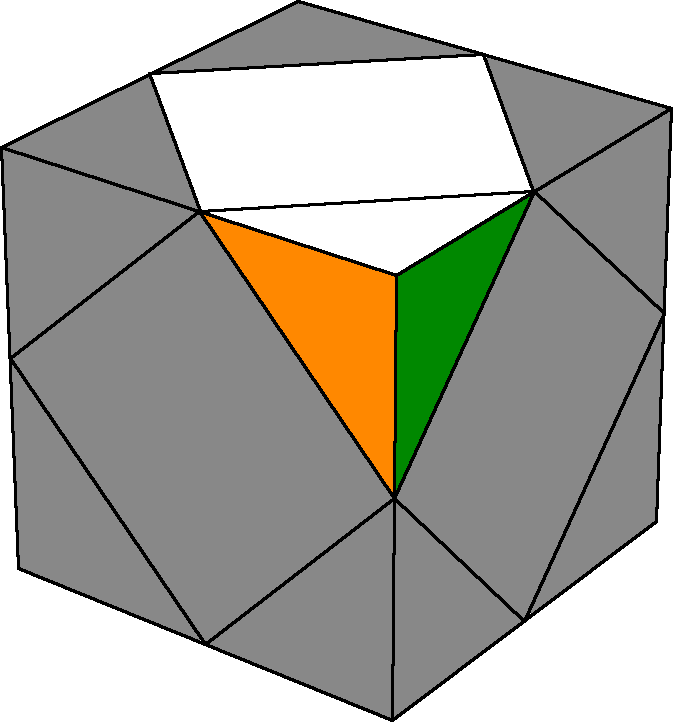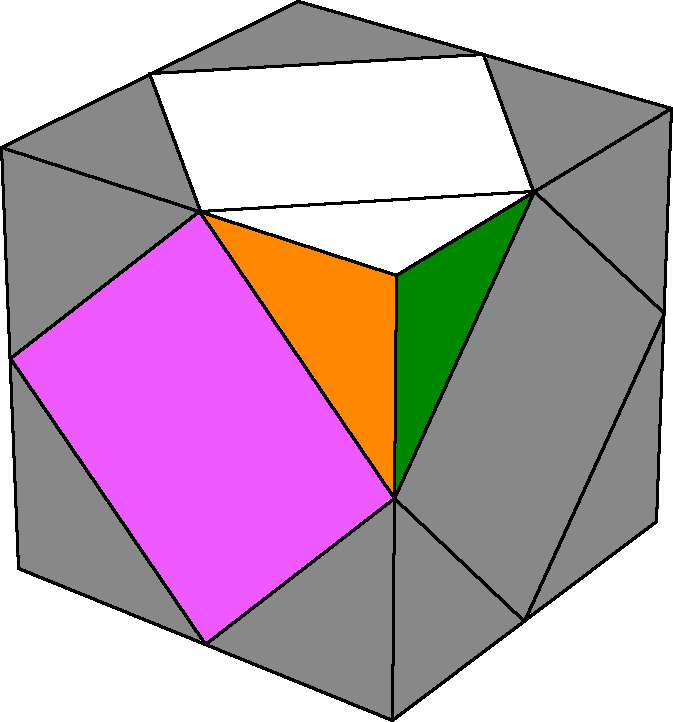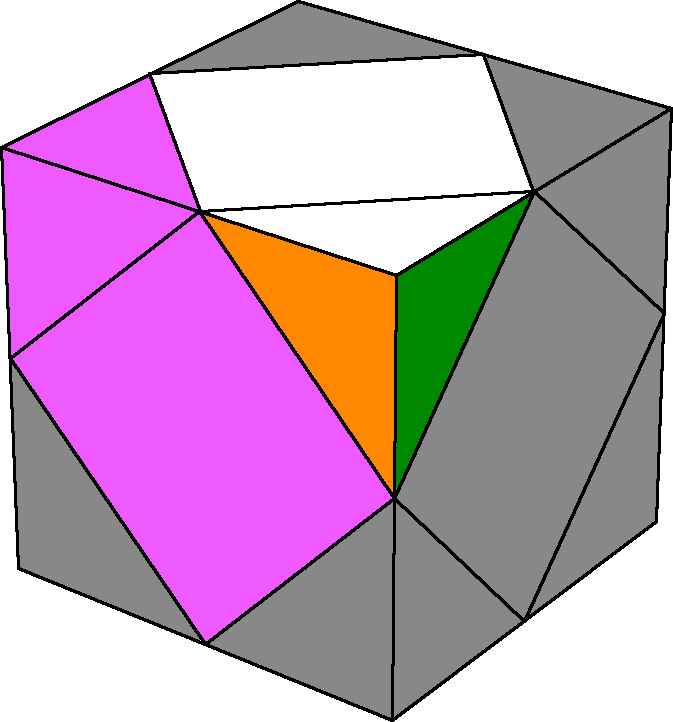
Attach the corner first, and then the center.

Attaching a Center, then a Corner

Attaching a center is pretty easy. Try experimenting, making sure that the pieces you have solved thus far never disconnect. It should take at most two moves.
Attaching the following corner piece isn't as easy. Using the compulsory piece insertion technique "open slot, insert piece, close slot", we can attach the final corner of our Petrus Block. First, try positioning the corner in the position as indicated at left.
Positioning this corner here is the perfect setup for our open, position, and close technique. By doing r f r', the corner becomes attached to the block, completing it.

Once attached, the corner is in the correct position ("permutation") but may not be twisted ("oriented") correctly. Here are the possibilities and how to solve each unsolved case.

Solved	Clockwise	Anticlockwise
Step is solved!	r f' r' l r f r'	r f' r' l' r f r'

The algorithms listed above work by first taking out the incorrect corner piece by undoing the corner insertion algorithm (applied as r f r'), twisting the corner to its correct orientation, and then putting the corner back, but this time, twisted the correct way.

Now, the Petrus Block should be solved! Here's the other way of solving the last two pieces of the Petrus Block. If you don't care to read, click here to jump to Step Two: The Welder's Mask.

Attaching a Corner, then a Center

Attaching a corner to the 1a block is very easy and takes at most three moves. Experiment! Make sure that the 1a block never disconnects.
Attaching the following center piece can be difficult at first, but the task becomes easy once you get the hang of it. Luckily, the final center of the Petrus Block can be solved in at most four moves.
However, as optimality isn't our ultimate goal in this tutorial, to make this process both easy and efficient, here is a more streamlined approach.

First, position the final center on the opposite side of where it belongs, as shown in the image. This should take at most one move.
Then, holding the Skewb as the image shows, use the Sledgehammer algorithm: f' r f r'.

The Sledgehammer (or simply "Sledge") and its inverse (the Hedgeslammer, or "Hedge") are arguably the most important of all Skewb algorithms.

Now, the Petrus Block should be solved!


Step Two: The Welder's Mask

In this step, we'll finish the top face, depicted as the white face.

There are three particularly cool things about this step:

• This step only uses f and r turns, which don't disrupt the Petrus Block in the top left.
• These corners are not interchangeable.
• The bottom layer corners will end up in the right positions.

As an added bonus, each Welder's Mask case can be optimally solved using f and r turns in six moves or less.

We will first position the corners in the correct locations, and then orient them with the use of four short algorithms.

Permuting the U Corners

In the picture at left, the UFR and UBR corners, highlighted in pink, are the two positions that the remaining U-face corners must go to.
This substep can be completed intuitively in two moves or less.

You should be able to figure out intuitively which moves to do in order to permute these corners. Just make sure that the Petrus Block is NEVER broken during this step.

Here is how to do it, just in case:

If a U-face corner is in DFL, do f to move it to the UFR position.
If a U-face corner is in DBR, do f' to move it to the UFR position.
If a U-face corner is in DFR, do r to move it to the UBR position.
If a U-face corner is in DBL, do r' to move it to the UBR position.

Orienting the U Corners

Orienting the U-layer corners once they're permuted can be performed intuitively just as the initial permutation step. But for the algorithmic learner, through the use of four four-move algorithms (two of which orient the corner in the UFR slot, the remaining two of which orient the corner in the UBR slot), this substep can be performed in eight moves or less. Here are the algorithms now:

UFR Anticlockwise	UFR Clockwise	UBR Anticlockwise	UBR Clockwise
r f r' f'	f r f' r'	r' f' r f	f' r' f r

Step Three: Last Four Centers

Your Skewb will have either 0, 3, or 4 unsolved centers at this stage.
If your Skewb has 0 unsolved centers (that is, all of your Skewb's centers are solved) proceed to Step Four by clicking here.

There are a total of six unsolved cases for this step. Use y rotations so that your Skewb's centers are being solved as the pictures denote.

3 Unsolved Centers
(hover for hidden faces)

U R-L-D	Oa R-D-F	Ob R-F-D
f' r f r' y2 f' r f r'	y2 r f r' f' y' f' r' f r	y f' r' f r y r f r' f'

4 Unsolved Centers
(hover for hidden faces)

H F-B, R-D	Za F-R, B-D	Zb F-D, R-B
f' r f r'	(r f r' f')(r f r' f')(r f r' f')	(f' r' f r)(f' r' f r)(f' r' f r)

Step Four: Corners of the Last Layer

At this stage, the only thing left to do is to correctly twist the corners of the bottom layer.

You could be the lucky 11.11% and have a solved Skewb. If so, congratulations! For the other 88.89% of us, we are equally likely to have either of two unsolved cases.
To solve the corners of the last layer, we will use the Sledgehammer f' r f r' various numbers of times.

Peanut	(f' r f r')(f' r f r') y (f' r f r')(f' r f r')
Pi	(f' r f r')(f' r f r')

It should be noted that for Peanut, the D-face stickers should be visible as pictured before executing the corresponding algorithm. For Pi, rotate the puzzle so that there are two D-face stickers on the B face before executing the corresponding algorithm.


After this, your Skewb should be solved! Hooray!